（译）缓存参数无关算法

缓存参数无关算法笔记

参考链接：

Cache Oblivious Introduce blog

Cache Oblivious paper

假设硬盘存在 M bits，以 B bits 作为分页大小，缓存按页加载，介绍相关的缓存参数无关的命中算法，这里的参数指 B

转化问题： N 个整数，按 B 个一页，求最快找到 N 所在页的算法

算法低效但是参数无关: 二分查找

假设 N 个整数本身是有序的，采用方法：总长 O(N) 所以计算查找次数为 O(logN -logB)，因为二分范围降到 B 时直接取出该页

参数无关是因为该算法并不知晓 B 的值，它只是按照标准的二分查找去搜（调用方是缓存，它load B 页时会去查到真正的所需值来停止二分，这对二分算法本身不可见）

非低效，但是参数相关: B-Tree

假设一开始知晓 B 的值，那么就可以达到 O(log[B]N) (中括号代表底数)，具体如下

首先把 list 转成 B 树：也就是说每个节点有 B 个元素，统一节点的元素是有序的，不同节点之间是整体有序的，每个节点上 B 个元素会产生 B+1 个分支，这样生成树之后，每下降一层间隔就会减少 B 倍(也就是砍掉了其他分支，相当于树的第二层取了节点作为新树), 那时间复杂度就是 O(logN/logB) = O(log[B]N)

非低效且参数无关算法: van Emde Boas layout

传统的二分搜索树的特性决定了每次搜索都是 O(logN - logB)，这显然不合期望，van Emde Boas layout 算法使用了一种很好的递归方式来排序，从而使得每次分页的查询都包含接下来可能要查的几个节点，从而提高命中率。

简洁概念

假设存在树高 H = 2^K.

概念展开

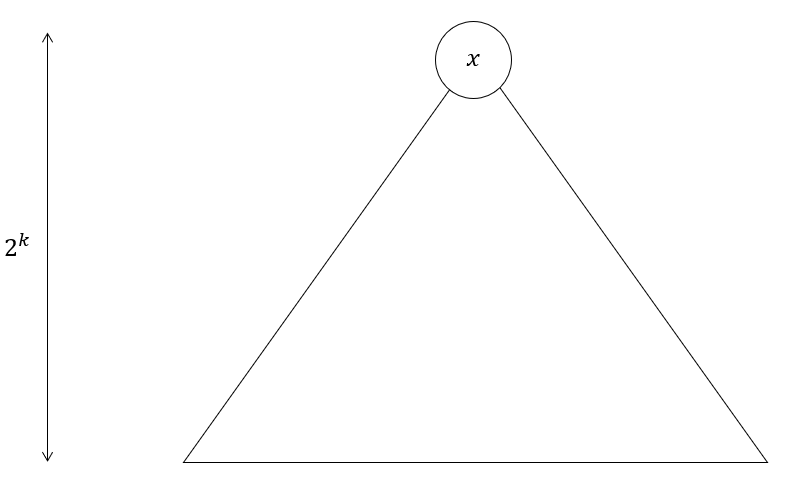
假设现在有一棵完全二叉树 H = 2^K，以 x 作为 root 节点，而我们的目的是计算出二叉树顶点的一种排列： L(x, k)

横切 2^(k-1) 和 2^(k-1) + 1 两层之间的枝，然后我们将得到这样的结果
- n=2^(h/2) 个 2^(K-1) 高的小完全二叉树这些二叉树是从上面的节点断开后生成的，分别以 l1..ln 作为根节点。
- 以及以 root 作为根节点的 2^(K-1) 高的根树。

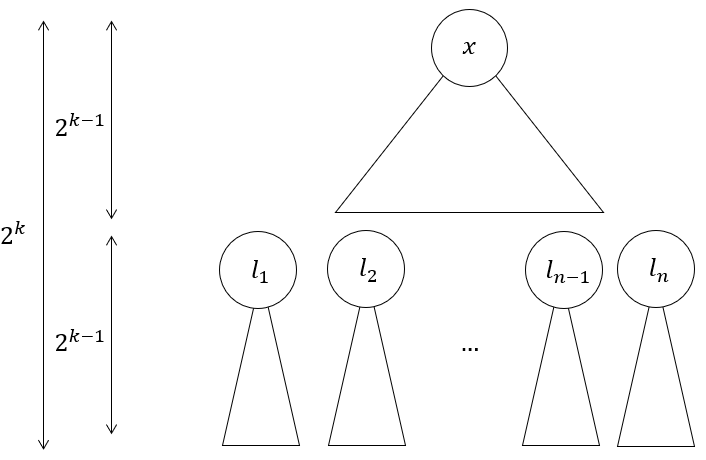
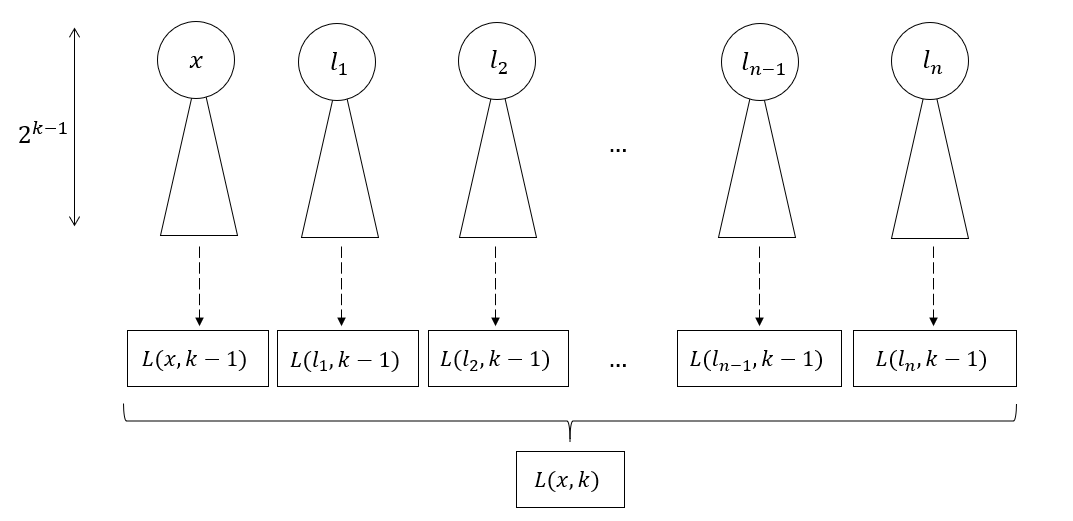
以 x 根节点和 k 值得到的这 n+1 个 BST的调用函数我们称为 L(x, k)
将它们排列好后返回（顺序不重要）

Sierpinski triangles, atoms and time

为了更好的解释接下来如何实现这种构造，首先给出一个直观的演示，它很像 Sierpinski 三角，如下：

同过 Sierpinski 三角我们大致能得到一种限制深度的递归，这使得这个递归更加偏像 BFS 而不是 DFS。

具体一点来说，我们引入 t 变量作为限制的递归深度，并引入概念 atom 代表递归深度为 t 时的子树单元。举例来说，递归深度 t 为 0 的时候，atom 是整个树。

接下来，当 t = 1 我们得到上面提到过的 2^(K-1) 高的子树，这时的 atoms 指的就是这些子树。

继续提高 t 递归深度，得到一批 2^(K-2) 的 atoms。

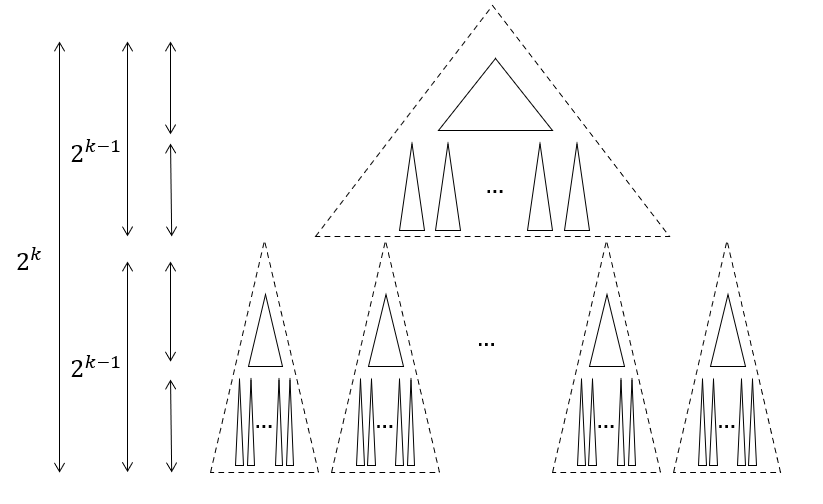
随着递归深度的提高最终 atoms 会变成最小的子树单元也就是一个个独立的节点。这一过程表明我们通过限制 t 即递归的深度可以得到不同程度精细的 atoms，综上可以获取如下推论

In the final layout, we can choose any resolution to look at the layout. All vertices in any atom at this resolution will be in a contiguous segment.

Algorithm

假设页面大小是 B。每步进一次，原子的高度减半。这样 B 和原子的关系就构建出来了，无论 B 是多大，只要每次我们使得得到的原子群高度为 O(logB) 即可，这样他就可以塞进一页(2^(logB) = B)当中去。

现在来算下搜索复杂度：它会首先遍历第一个 atom 子树，直到遍历完该子树的所有节点，然后继续使用相同的遍历去遍历下一个 atom 子树，每次这样的遍历花费 O(logB) 次步进，然后未划分子树前我们知道整棵大树需要 O(logN) 次遍历，所以我们可以算出来一共有 O(logN / logB) = O(log[B]N) 个 atom，这个数量也同时就是我们需要 access page 的次数。