CSAPP | ReZero's blog

Not be the real thing

digit might be overfolw
float will not be overflow, but could lost precision

Memory

RAM: Random am

Bit

Exclusive-Or(XOR) A ^ B

Union | //并

Complement ~ //补

Intersection & //交

Symmetric difference ^ //差

Integer

Unsigned：

$$ B2U(X)=\sum_{i=0}^{w-1}x_i*2^i $$

Signed：

$$ B2T(X)=-x_{w-1}2^{w-1}+\sum_{i=0}^{w-2}x_i2^i $$

Type Conversion

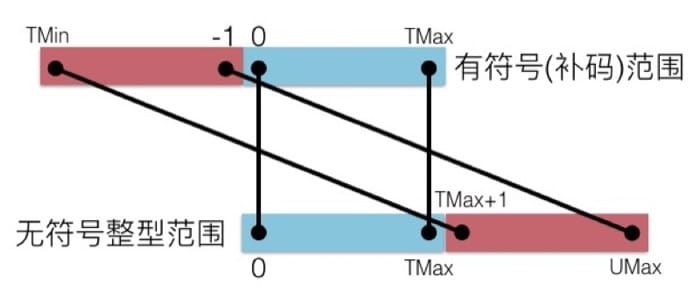
If not set keyword(unsigned) in C, then must use U follow number to change the default value(signed) such as 15213U

Conversion mutual

Byte will not changed, but change the interpreted way.
Both all will be convert into unsigned if include one unsigned.

Type extension & Intercept

Extend: from short to int
- unsigned: plus 0
- signed: plus sign
Intercept: from unsigned int to unsigned short
- unsigned: mod operation
- signed: almost mod operation

Calculate & Overflow

Both w bit unsigned number mutual plus, and get a result w+1 bit. Then it will lose the highest bit, just like mod operation:

$$s=UAdd_w(u,v)=u+v ; mod ; 2^w$$

So as signed number, but change the sign symbol.

Float

$$\sum_{k=-j}^ib_k\times 2^k$$

IEEE standard

$$(-1)^s ; M ; 2^E$$

s is sign symbol, M always be [1.0, 2.0) decimal, and E is power.

Exp related E(not equal must, as the limit of bit count), frac related M(So as E)

Normalized Values

$$v=(-1)^s ; M ; 2^E$$

E = Exp - Bias
Exp: exp encode area unsigned digit
Bias: as k is exp encode count, which means

$$2^{k-1} - 1$$

- single precision: 127 (Exp:1...254,E:-126...127)
- double precision: 1023 (Exp:1...2046, E:-1022...1023)

Note: Exp encode only need unsigned digit to operate.

For M, it must begin with 1: M = 1.xxx…x2, and xxx means frac(frac = 000.00 corresponding minium M = 1.0), when frac=111…1, M will be infinite close to 2.0

For Example: Float F = 15213.0

$$15213_{10}=11101101101101_2=1.1101101101101_2 \times 2^{13}$$

So the frac part is the point behind, and Exp = E + Bias = 12 + 127 = 140 = 10001100(b)

0 10001100 11011011011010000000000
s   exp             frac

Denormalized Values

E = 1 - Bias And M = 0.xxx...x2 But others not changed.

exp = 000…0 & frac = 000…0 : 0
exp = 000…0 & frac != 000…0 : infinite to 0
exp = 111…1 & frac = 000..0 infinite
exp = 111…1 & frac != 000…0 NaN

Real sample

    s exp  frac   E   值
------------------------------------------------------------------
    0 0000 000   -6   0   # 这部分是非规范化数值，下一部分是规范化值
    0 0000 001   -6   1/8 * 1/64 = 1/512 # 能表示的最接近零的值
    0 0000 010   -6   2/8 * 1/64 = 2/512 
    ...
    0 0000 110   -6   6/8 * 1/64 = 6/512
    0 0000 111   -6   7/8 * 1/64 = 7/512 # 能表示的最大非规范化值
------------------------------------------------------------------
    0 0001 000   -6   8/8 * 1/64 = 8/512 # 能表示的最小规范化值
    0 0001 001   -6   9/8 * 1/64 = 9/512
    ...
    0 0110 110   -1   14/8 * 1/2 = 14/16
    0 0110 111   -1   15/8 * 1/2 = 15/16 # 最接近且小于 1 的值
    0 0111 000    0   8/8 * 1 = 1
    0 0111 001    0   9/8 * 1 = 9/8      # 最接近且大于 1 的值
    0 0111 010    0   10/8 * 1 = 10/8
    ...
    0 1110 110    7   14/8 * 128 = 224
    0 1110 111    7   15/8 * 128 = 240   # 能表示的最大规范化值
------------------------------------------------------------------
    0 1111 000   n/a  无穷               # 特殊值

Note:

exp = 0000(Denormalize) 1/8 is the distance

  原数值       舍入结果    原因
8949999      2.89    不到一半，正常四舍五入
8950001      2.90    超过一半，正常四舍五入
8950000      2.90    刚好在一半时，保证最后一位是偶数，所以向上舍入
8850000      2.88    刚好在一半时，保证最后一位是偶数，所以向下舍入

  十进制    二进制     舍入结果  十进制    原因
又 3/32  10.00011   10.00     2      不到一半，正常四舍五入
又 3/16  10.00110   10.01  2 又 1/4   超过一半，正常四舍五入
又 7/8   10.11100   11.00     3      刚好在一半时，保证最后一位是偶数，所以向上舍入
又 5/8   10.10100   10.10  2 又 1/2   刚好在一半时，保证最后一位是偶数，所以向下舍入

Data in Memory

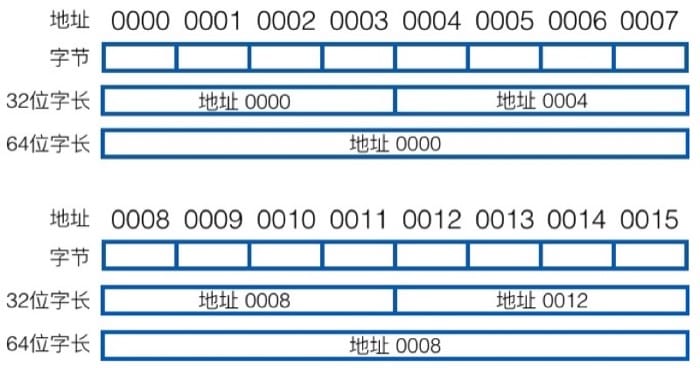
Internet: Big Endian

x86 OR ARM: Little Endian

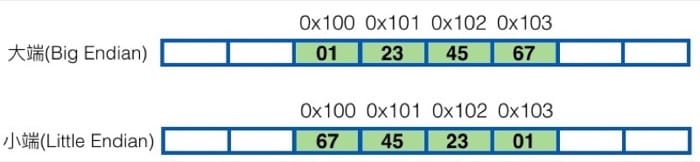
// Check the num format
typedef unsigned char *pointer;
void show_bytes(pointer start, size_t len) {
	size_t i;
	for (i = 0; i < len; i++)
		printf("%p\t0x%.2x\n", start+i, start[i]);
	printf("\n");
}

%p: point, %x: Hex, Execute as:

int a = 15213;
printf("int a = 15213;\n");
show_bytes((pointer) &a, sizeof(int));

Basic

C2M

.c (gcc -0g 0S) -> .s
.s (gcc OR as) -> .o
.o (with lib.a operated by gcc OR ld) execute.

long plus(long x, long y);
void sumstore(long x, long y, long *dest)
{
    long t = plus(x, y);
    *dest = t;
}

appropriate code:

sumstore:
    pushq   %rbx
    movq    %rbx, %rbx
    call    plus
    movq    %rax, (%rbx)
    popq    %rbx
    ret

Processor:

Storage: Memory & Register
Calc: Memory & Register
Transfer: condition call OR condition branch

// C 代码
*dest = t;
// 对应的汇编代码
movq    %rax, (%rbx)
// 对应的对象代码
0x40059e:   46 89 03

Assembly

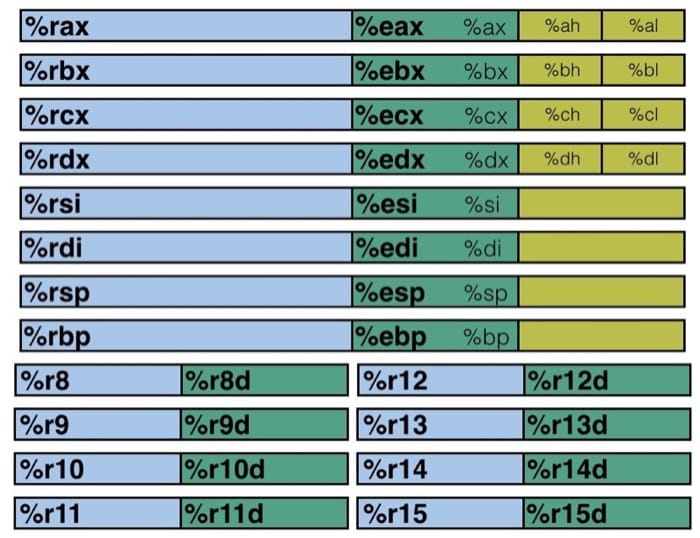
General purpose register

%rax(%eax) 用于做累加
%rcx(%ecx) 用于计数
%rdx(%edx) 用于保存数据
%rbx(%ebx) 用于做内存查找的基础地址
%rsi(%esi) 用于保存源索引值
%rdi(%edi) 用于保存目标索引值

%rsp(%esp) 和 %rbp(%ebp) 则是作为栈指针和基指针来使用的

movq Sour:[Imm|Reg|Mem], Dest[Reg|Mem] (But No Mem Mem)

D(Rb, Ri, S) -> Mem[Reg[Rb]+S*Reg[Ri]+D]

D - 常数偏移量
Rb - 基寄存器
Ri - 索引寄存器，不能是 %rsp
S - 系数
(Rb, Ri) -> Mem[Reg[Rb]+Reg[Ri]]
D(Rb, Ri) -> Mem[Reg[Rb]+Reg[Ri]+D]
(Rb, Ri, S) -> Mem[Reg[Rb]+S*Reg[Ri]]

long m12(long x)
{
    return x * 12;
}

leaq (%rdi, %rdi, 2), %rax # t <- x+x*2
salq $2, %rax              # return t << 2

More orders:

addq Src, Dest -> Dest = Dest + Src
subq Src, Dest -> Dest = Dest - Src
imulq Src, Dest -> Dest = Dest * Src
salq Src, Dest -> Dest = Dest << Src
sarq Src, Dest -> Dest = Dest >> Src
shrq Src, Dest -> Dest = Dest >> Src
xorq Src, Dest -> Dest = Dest ^ Src
andq Src, Dest -> Dest = Dest & Src
orq Src, Dest -> Dest = Dest | Src
incq Dest -> Dest = Dest + 1
decq Dest -> Dest = Dest - 1
negq Dest -> Dest = -Dest
notq Dest -> Dest = ~Dest

Flow Control

临时数据存放在 (%rax, …)
运行时栈的地址存储在 (%rsp) 中
目前的代码控制点存储在 (%rip, …) 中
目前测试的状态放在 CF, ZF, SF, OF 中

Condition & Jump

CF: Carry Flag (针对无符号数)
ZF: Zero Flag
SF: Sign Flag (针对有符号数)
OF: Overflow Flag (针对有符号数)

long absdiff(long x, long y)
{
    long result;
    if (x > y)
        result = x-y;
    else
        result = y-x;
    return result;
}

%rdi save x，%rsi save y， %rax save return.

absdiff:
    cmpq    %rsi, %rdi
    jle     .L4
    movq    %rdi, %rax
    subq    %rsi, %rax
    ret
.L4:    # x <= y
    movq    %rsi, %rax
    subq    %rdi, %rax
    ret

long absdiff_goto(long x, long y)
{
    long result;
    int ntest = x <= y;
    if (ntest) goto Else;
    result = x-y;
    goto Done;
Else:
    result = y-x;
Done:
    return result;
}

val = Test ? Then_Expr : Else_Expr;
val = x>y ? x-y : y-x;

To Goto

	ntest = !Test;
	if (ntest) goto Else;
	value = Then_Expr;
	goto Done;
Else:
	val = Else_Expr;
Done:
	...

Calc all to avoid the reset assembly line operation

result = Then_Expr;
eval = Else_Expr;
nt = !Test;
if (nt) result = eval;
return result;

Such as:

absdiff:
    movq    %rdi, %rax  # x
    subq    %rsi, %rax  # result = x-y
    movq    %rsi, %rdx
    subq    %rdi, %rdx  # eval = y-x
    cmpq    %rsi, %rdi  # x:y
    cmovle  %rdx, %rax  # if <=, result = eval
    ret

Not suited:

Much more calc in the two branches
val = p ? *p : 0; some interesting happen
val = x > 0? x *= 7: x *= 3 x will change

Do While

// Do While 的 C 语言代码
long pcount_do(unsigned long x)
{
    long result = 0;
    do {
        result += x & 0x1;
        x >>= 1;
    } while (x);
    return result;
}
// Goto 版本
long pcount_goto(unsigned long x)
{
    long result = 0;
loop:
    result += x & 0x1;
    x >>= 1;
    if (x) goto loop;
    return result;
}

To assembly:

    movl    $0, %eax    # result = 0
.L2:                    # loop:
    movq    %rdi, %rdx
    andl    $1, %edx    # t = x & 0x1
    addq    %rdx, %rax  # result += t
    shrq    %rdi        # x >>= 1
    jne     .L2         # if (x) goto loop
    rep; ret

// C Code
do
	Body
	while (Test);
// Goto Version
loop:
	Body
	if (Test)
		goto loop

// C While version
while (Test)
	Body
// Goto Version
	goto test;
loop:
	Body
test:
	if (Test)
		goto loop;
done:

Turn on -01 Optimize option, While will be transfer into Do-While, then transfer into Goto, Because Do-While execute so faster, which much more suit CPU calc model.

// For
for (Init; Test; Update)
	Body
	
// While Version
Init;
while (Test) {
	Body
	Update;
}

Switch:

long switch_eg (long x, long y, long z){
	long w = 1;
	switch (x) {
		case 1:
			w = y*z;
			break;
		case 2:
			w = y/z;
			// fall through
		case 3:
			w += z;
			break;
		case 5:
		case 6:
			w -= z;
			break;
		default:
			w = 2;
	}
	return w;
}

We will use jump table:
%rdi is x, %rsi is y, %rdx is z, %rax is return

switch_eg:
    movq    %rdx, %rcx
    cmpq    $6, %rdi    # x:6
    ja      .L8
    jmp     *.L4(, %rdi, 8)

--------------
Jump table as
--------------

.section    .rodata
    .align 8
.L4:
    .quad   .L8 # x = 0
    .quad   .L3 # x = 1
    .quad   .L5 # x = 2
    .quad   .L9 # x = 3
    .quad   .L8 # x = 4
    .quad   .L7 # x = 5
    .quad   .L7 # x = 6

Process call

Delivery Control: How to begin, and return back the begin
Delivery Data: Args and return value.
Memory Manage: How to free and malloc memory.

Stack Structure

%rsp is stack point

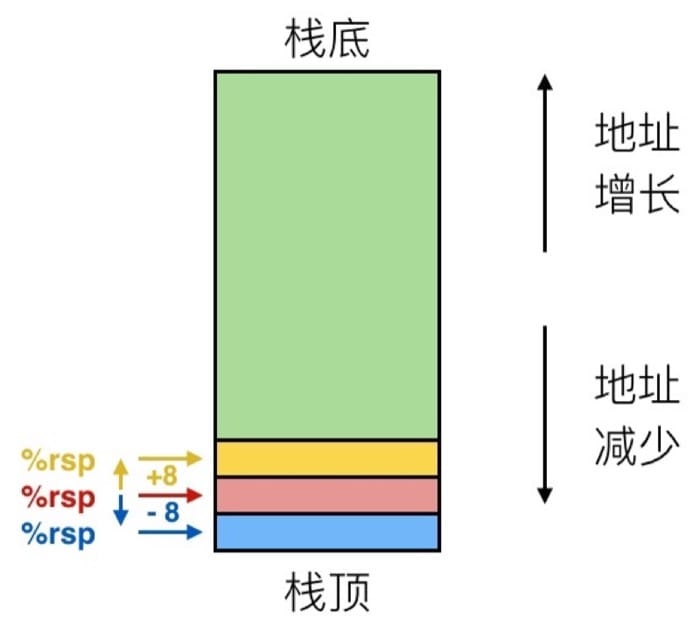
Call ways

// multstore 函数
void multstore (long x, long, y, long *dest)
{
    long t = mult2(x, y);
    *dest = t;
}
// mult2 函数
long mult2(long a, long b)
{
    long s = a * b;
    return s;
}


// Assembly
0000000000400540 <multstore>:
    # x 在 %rdi 中，y 在 %rsi 中，dest 在 %rdx 中
    400540: push    %rbx            # 通过压栈保存 %rbx
    400541: mov     %rdx, %rbx      # 保存 dest
    400544: callq   400550 <mult2>  # 调用 mult2(x, y)
    # t 在 %rax 中
    400549: mov     %rax, (%rbx)    # 结果保存到 dest 中
    40054c: pop     %rbx            # 通过出栈恢复原来的 %rbx
    40054d: retq                    # 返回
0000000000400550 <mult2>:
    # a 在 %rdi 中，b 在 %rsi 中
    400550: mov     %rdi, %rax      # 得到 a 的值
    400553: imul    %rsi, %rax      # a * b
    # s 在 %rax 中
    400557: retq                    # 返回

call: 将当前的IP 或者 CS:IP 压入栈中, 跳转到指定位置
ret : 用栈中所保存的数据赋值给IP的，跳转回来

参数没有超过六个，那么会放在：%rdi, %rsi, %rdx, %rcx, %r8, %r9 中。

如果超过了，会另外放在一个栈中。而返回值会放在 %rax 中

A Frame will be assigned to every call process by on stack which include three as follows:

返回信息
本地存储（如果需要）
临时空间（如果需要）

Call then alloc, free when return.

x86_64/Linux, fixed in that:

Argument Build: 需要使用的参数
如果不能保存在寄存器中，会把一些本地变量放在这里
已保存的寄存器上下文
老的栈帧的指针（可选）

While caller include:

返回地址（因为 call 指令被压入栈的）
调用所需的参数

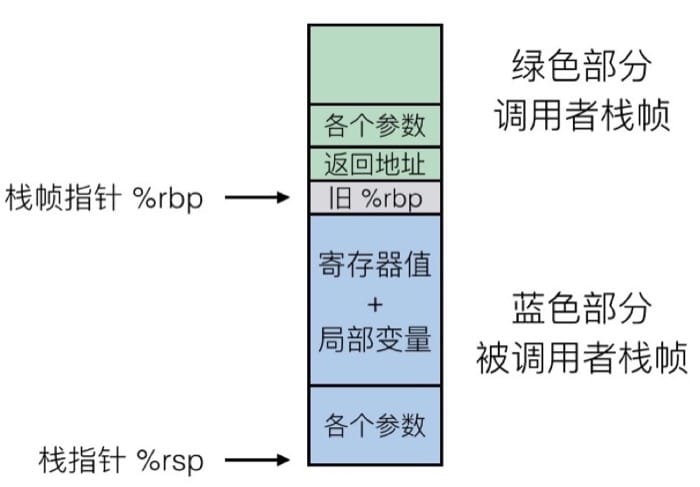
Recursive

long pcount_r(unsigned long x) {
	if (x == 0)
		return 0;
	else
		return (x & 1) + pcount_r(x >> 1);
}

pcount_r:
    mov     $0, %eax
    testq   %rdi, %rdi
    je      .L6
    push    %rbx
    movq    %rdi, %rbx
    andl    $1, %ebx
    shrq    %rdi
    call    pcount_r
    addq    %rbx, %rax
    popq    %rbx
.L6:
    rep; ret

Data Storage

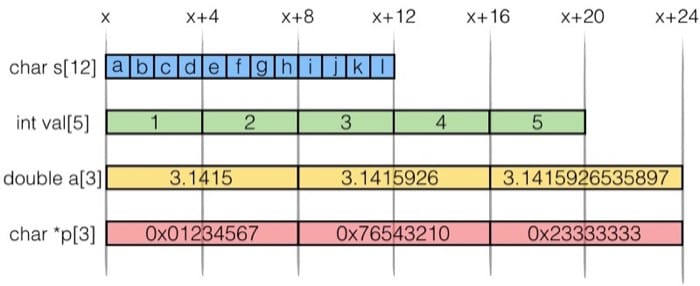
Struct:

struct rec 
{
    int a[4];
    size_t i;       
    struct rect *next;
};

struct S1
{
    char c;
    int i[2];
    double v;
} *p;

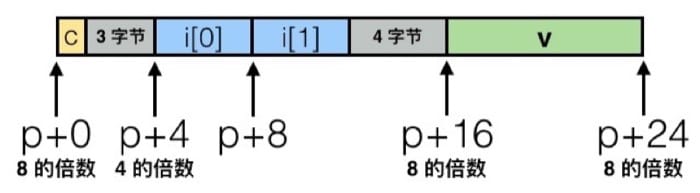
Align theory:

Win: 如果数据类型需要 K 个字节，那么地址都必须是 K 的倍数

Linux: 2字节数据类型的地址必须为2的倍数，较大的数据类型（int,double,float）的地址必须是4的倍数

So we could design struct like this(big bit number on the front):

Cache overflow

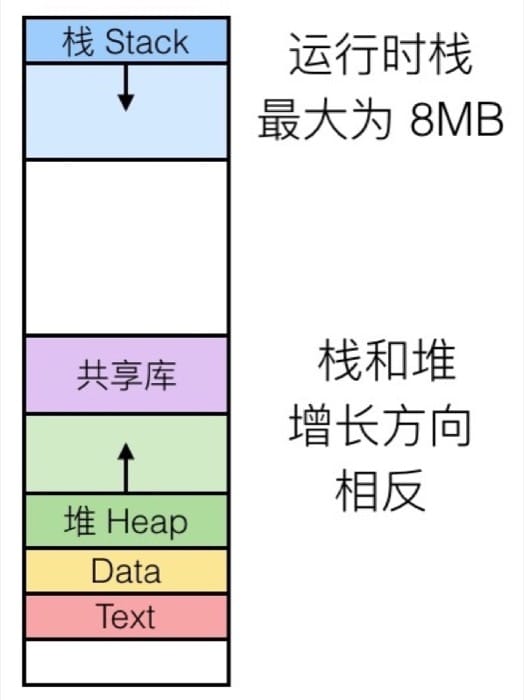
最上面是运行时栈，有 8MB 的大小限制，一般用来保存局部变量。然后是堆，动态的内存分配会在这里处理，例如 malloc(), calloc(), new() 等。然后是数据，指的是静态分配的数据，比如说全局变量，静态变量，常量字符串。最后是共享库等可执行的机器指令，这一部分是只读的。

可以见到，栈在最上面，也就是说，栈再往上就是另一个程序的内存范围了，这种时候我们就可以通过这种方式修改内存的其他部分了。

Sample:

void echo() {
	char buf[4]; // 太小
	gets(buf);
	puts(buf);
}
void call_echo() {
	echo();
}


00000000004006cf <echo>:
    4006cf: 48 83 ec 18         sub   $0x18, %rsp
    4006d3: 48 89 e7            mov   %rsp, %rdi
    4006d6: e8 a5 ff ff ff      callq 400680 <gets>
    4006db: 48 89 e7            mov   %rsp, %rdi
    4006de: e8 3d fe ff ff      callq 400520 <puts@plt>
    4006e3: 48 83 c4 18         add   $0x18, %rsp
    4006e7: c3                  retq
# call_echo 部分
    4006e8: 48 83 ec 08         sub   $0x8, %rsp
    4006ec: b8 00 00 00 00      mov   $0x0, %eax
    4006f1: e8 d9 ff ff ff      callq 4006cf <echo>
    4006f6: 48 83 c4 08         add   $0x8, %rsp
    4006fa: c3                  retq

0x18 not 4, before 4006d6

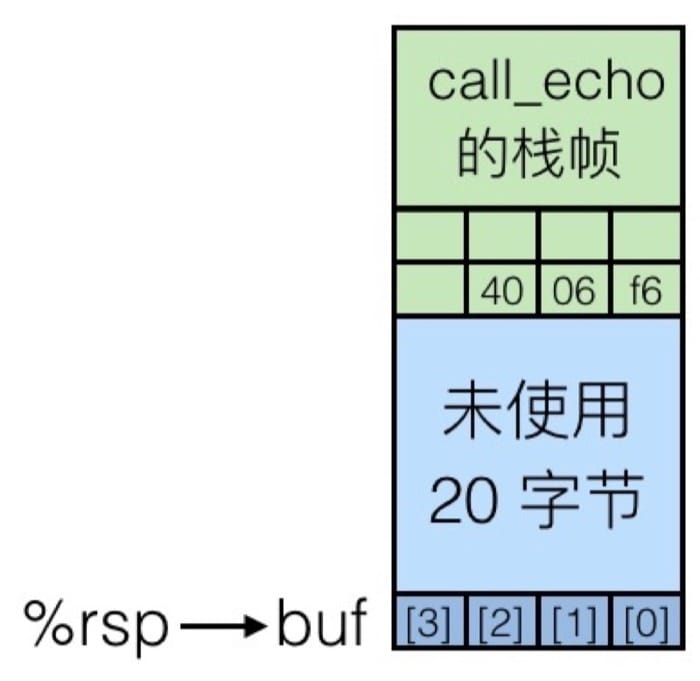
See, the call_echo frame saved 4006f6 order, and when we type 01234567890123456789012

Cache like this(No Segment Fault):

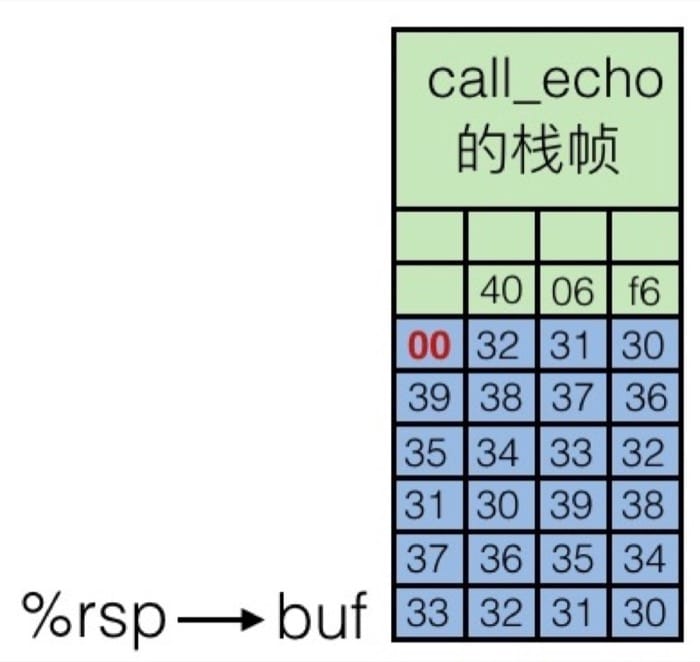
but more will override the 4006f6 get 400034(the back next order)

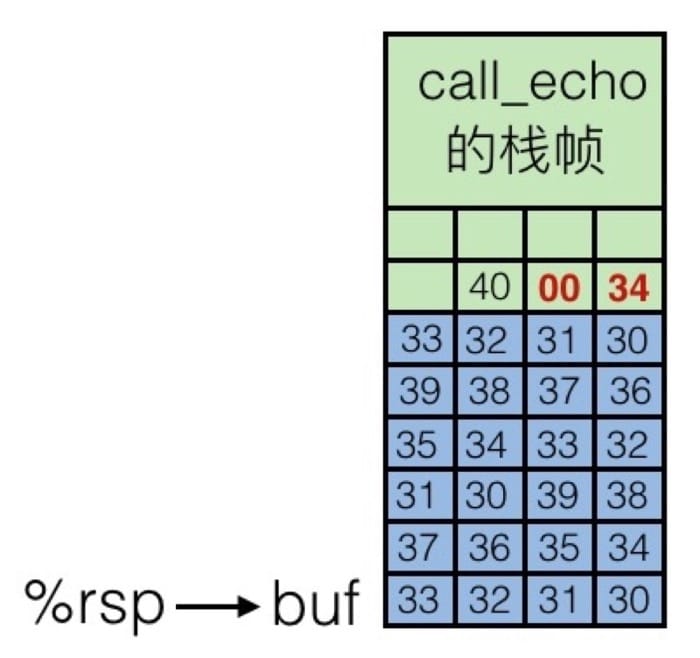
返回导向编程: 可以利用修改已有的代码，来绕过系统和编译器的保护机制，攻击者控制堆栈调用以劫持程序控制流并执行针对性的机器语言指令序列（称为Gadgets）。每一段 gadget 通常结束于 return 指令，并位于共享库代码中的子程序。系列调用这些代码，攻击者可以在拥有更简单攻击防范的程序内执行任意操作。

Optimize

// 把 nxn 的矩阵 a 的每一行加起来，存到向量 b 中
void sum_rows1(double *a, double *b, long n)
{
    long i, j;
    for (i = 0; i < n; i++)
    {
        b[i] = 0;
        for (j = 0; j < n; j++)
            b[i] += a[i*n + j];
    }
}

// 把 nxn 的矩阵 a 的每一行加起来，存到向量 b 中
void sum_rows2(double *a, double *b, long n)
{
    long i, j;
    for (i = 0; i < n; i++)
    {
        double val = 0;
        for (j = 0; j < n; j++)
            val += a[i*n + j];
        b[i] = val;
    }
}

To remove quote memory

// 把 nxn 的矩阵 a 的每一行加起来，存到向量 b 中
void sum_rows2(double *a, double *b, long n)
{
    long i, j;
    for (i = 0; i < n; i++)
    {
        double val = 0;
        for (j = 0; j < n; j++)
            val += a[i*n + j];
        b[i] = val;
    }
}

# sum_rows2 内循环
.L10:
    addsd   (%rdi), %xmm0   # 浮点数载入 + 加法
    addq    $9, %rdi
    cmpq    %rax, %rdi
    jne     .L10

这个问题，如果不是对处理器执行指令的机制有一定了解的话，可能会难以理解。

现代处理器普遍采用超标量设计，也就是基于流水线来进行指令的处理，也就是说，当执行当前指令时，接下来要执行的几条指令已经进入流水线的处理流程了。

这个很重要，对于顺序执行来说，不会有任何问题，但是对于条件分支来说，在跳转指令时可能会改变程序的走向，也就是说，之前载入的指令可能是无效的。这个时候就只能清空流水线，然后重新进行载入。为了减少清空流水线所带来的性能损失，处理器内部会采用称为『分支预测』的技术。

比方说在一个循环中，根据预测，可能除了最后一次跳出循环的时候会判断错误之外，其他都是没有问题的。这就可以接受，但是如果处理器不停判断错误的话（比方说代码逻辑写得很奇怪），性能就会得到极大的拖累。

分支问题有些时候会成为最主要的影响性能的因素，但有的时候其实很难避免。

Base concept

容量 Capacity = 每个扇区的字节数(bytes/sector) x 磁道上的平均扇区数(avg sectors/track) x 磁盘一面的磁道数(tracks/surface) x 磁盘的面数(surfaces/platter) x 硬盘包含的磁盘数(platters/disk)

总的访问时间 Taccess = 寻址时间 Tavg seek + 旋转时间 Tavg rotation + 传输时间 Tavg transfer

主要决定访问时间的是寻址时间和旋转延迟；读取一个扇区的第一个比特是非常耗时的，之后的都几乎可以忽略不计；硬盘比 SRAM 慢 40,000 倍，比 DRAM 慢 2500 倍。

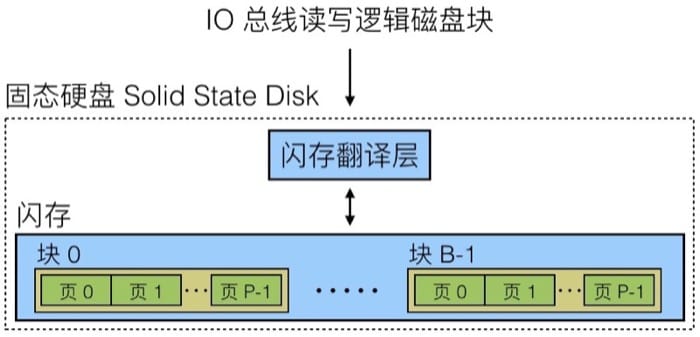
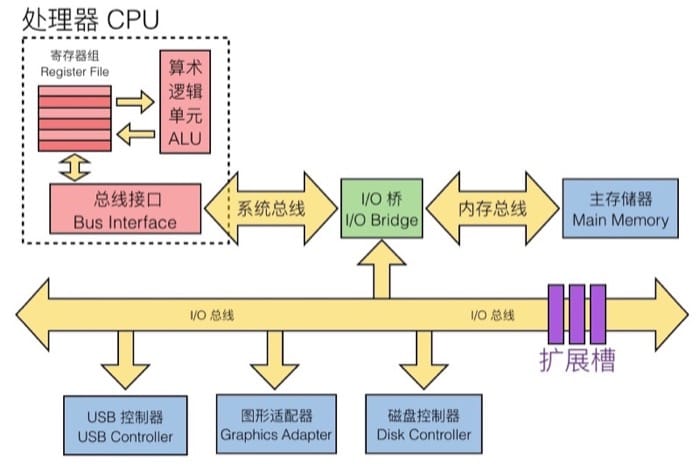
假设 CPU 需要从硬盘中读取一些数据，会给定指令，逻辑块编号和目标地址，并发送给磁盘控制器。然后磁盘控制器会读取对应的数据，并通过 DMA(direct memory access)把数据传输到内存中；传输完成后，磁盘控制器通过中断的方式通知 CPU，然后 CPU 完成之后的工作

Memory Hierarchy

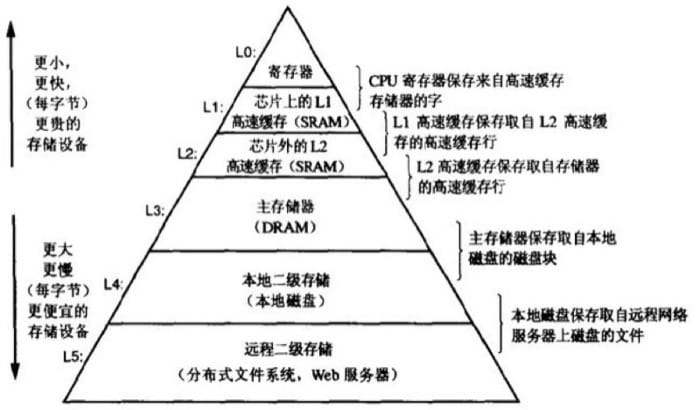
每一层都可以看作是下一层的缓存。利用局部性原理，程序会更倾向于访问第 k 层的数据，而非第 k+1 层，这样就减少了访问时间。

缓存类型	缓存内容	缓存位置	延迟(时钟周期)	管理者
寄存器	4-8 字节的字	CPU 内核	0	编译器
TLB	地址翻译	芯片 TLB	0	内存管理单元
L1 缓存	64 字节的块	芯片 L1 缓存	4	硬件
L2 缓存	64 字节的块	芯片 L2 缓存	10	硬件
虚拟内存	4 KB 的页	主存	100	硬件 + 操作系统
缓冲区缓存	文件的部分内容	主存	100	操作系统
磁盘缓存	磁盘扇区	磁盘控制器	100,000	磁盘固件
网络缓冲区缓存	文件的部分内容	本地磁盘	10,000,000	NFS 客户端
浏览器缓存	网页	本地磁盘	10,000,000	网络浏览器
Web 缓存	网页	远程服务器磁盘	1,000,000,000 Web	代理服务器

Cache miss

强制性失效(Cold/compulsory Miss): CPU 第一次访问相应缓存块，缓存中肯定没有对应数据，这是不可避免的
冲突失效(Confilict Miss): 在直接相联或组相联的缓存中，不同的缓存块由于索引相同相互替换，引起的失效叫做冲突失效
- 假设这里有 32KB 直接相联的缓存
- 如果有两个 8KB 的数据需要来回访问，但是这两个数组都映射到相同的地址，缓存大小足够存储全部的数据，但是因为相同地址发生了冲突需要来回替换，发生的失效则全都是冲突失效（第一次访问失效依旧是强制性失效），这时缓存并没有存满
容量失效(Capacity Miss): 有限的缓存容量导致缓存放不下而被替换，被替换出去的缓存块再被访问，引起的失效叫做容量失效
- 假设这里有 32KB 直接相联的缓存
- 如果有一个 64KB 的数组需要重复访问，数组的大小远远大于缓存大小，没办法全部放入缓存。第一次访问数组发生的失效全都是强制性失效。之后再访问数组，再发生的失效则全都是容量失效，这时缓存已经存满，容量不足以存储全部数据

Cache Memory

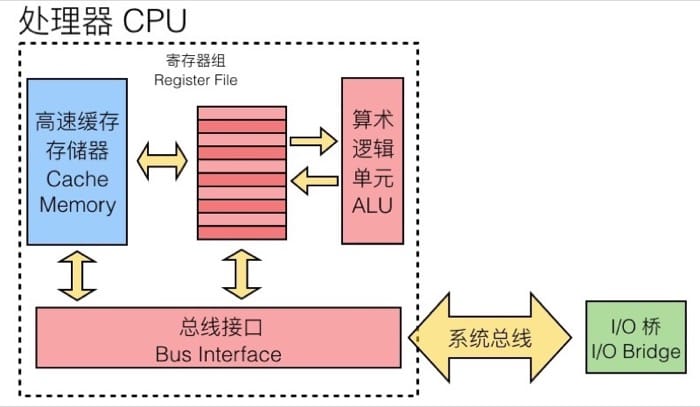
S 表示集合(set)数量
E 表示数据行(line)的数量
B 表示每个缓存块(block)保存的字节数目

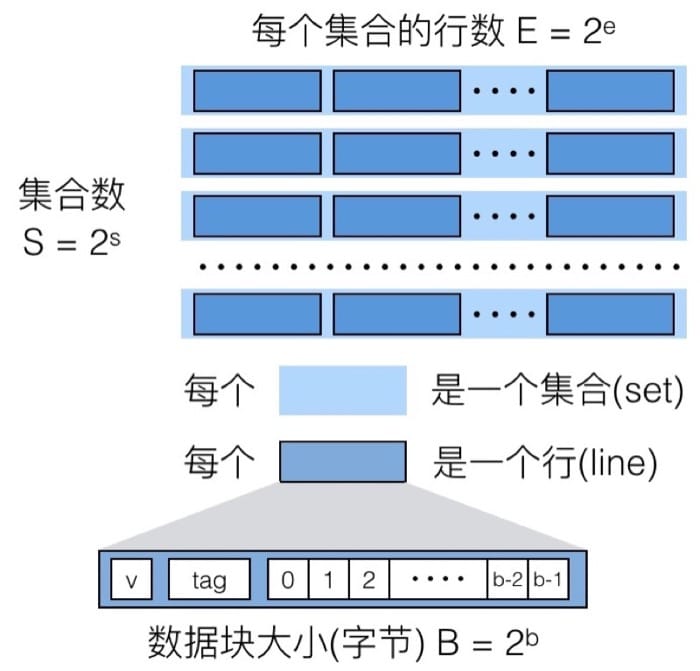
C = E * S * B

Read:

set index: set; tag: compare to every line; block offset: line offset

If E = 1: Direct Mapped Cache

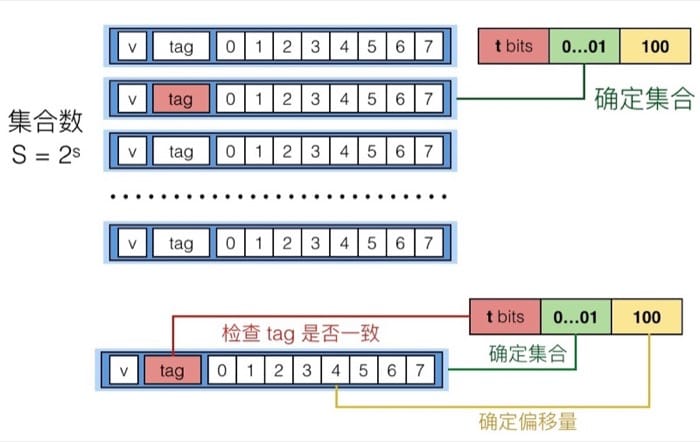
| 寻址空间是 M=16 字节，也就是 4 位的地址，对应 B=2, S=4, E=1

先从 set index 确定那个 set，然后看 valid 位，接着利用 t bits 分别和每个 line 的 tag 进行比较，如果匹配则命中，那么返回 4 5 位置的数据，如果不匹配，就需要替换，可以随机替换，也可以用 least recently used(LRU) 来进行替换

Complie

预处理器：将 C 语言代码(da.c)转化成 da.i 文件(gcc –E)，对应于预处理命令 cpp
编译器：C 语言代码(da.c, wang.c)经过编译器的处理(gcc -0g -S)成为汇编代码(da.s, wang.s)
汇编器：汇编代码(da.s, wang.s)经过汇编器的处理(gcc 或 as)成为对象程序(da.o, wang.o)
链接器：对象程序(da.o, wang.o)以及所需静态库(lib.a)经过链接器的处理(gcc 或 ld)最终成为计算机可执行的程序
加载器：将可执行程序加载到内存并进行执行，loader 和 ld-linux.so

head file search rule:

所有头文件的搜寻会从 -I 开始
然后找环境变量 C_INCLUDE_PATH, CPLUS_INCLUDE_PATH, OBJC_INCLUDE_PATH 指定的路径
再找默认目录(/usr/include, /usr/local/include, /usr/lib/gcc-lib/i386-linux/2.95.2/include 等等)

Object files

所谓的对象文件(Object File)实际上是一个统称，具体来说有以下三种形式：

可重定位目标文件 Relocatable object file (.o file)
- 每个 .o 文件都是由对应的 .c 文件通过编译器和汇编器生成，包含代码和数据，可以与其他可重定位目标文件合并创建一个可执行或共享的目标文件
可执行目标文件 Executable object file (a.out file)
- 由链接器生成，可以直接通过加载器加载到内存中充当进程执行的文件，包含代码和数据
共享目标文件 Shared object file (.so file)
- 在 windows 中被称为 Dynamic Link Libraries(DLLs)，是类特殊的可重定位目标文件，可以在链接(静态共享库)时加入目标文件或加载时或运行时(动态共享库)被动态的加载到内存并执行

Object format

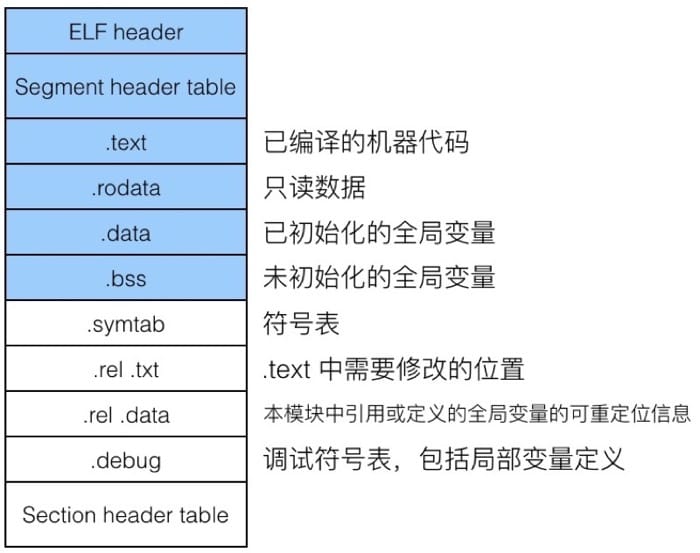
ELF header

包含 word size, byte ordering, file type (.o, exec, .so), machine type, etc

Segment header table

包含 page size, virtual addresses memory segments(sections), segment sizes

.text section

代码部分

.rodata section

只读数据部分，例如跳转表

.data section

初始化的全局变量

.bss section

未初始化的全局变量

.symtab section

包含 symbol table, procudure 和 static variable names 以及 section names 和 location

.rel.txt section

.text section 的重定位信息

.rel.data section

.data section 的重定位信息

.debug section

包含 symbolic debugging (gcc -g) 的信息

Section header table

每个 section 的大小和偏移量

链接器实际上会处理三种不同的符号，对应于代码中不同写法的部分：

全局符号 Global symbols
- 在当前模块中定义，且可以被其他代码引用的符号，例如非静态 C 函数和非静态全局变量
外部符号 External symbols
- 同样是全局符号，但是是在其他模块（也就是其他的源代码）中定义的，但是可以在当前模块中引用
本地符号 Local symbols
- 在当前模块中定义，只能被当前模块引用的符号，例如静态函数和静态全局变量
- 注意，Local linker symbol 并不是 local program variables

// 文件 main.c
int sum(int *a, int n);
int array[2] = {1, 2}; // 变量 array 在此定义
int main() // 定义了一个全局函数
{
    int val = sum(array, 2);
    // val 是局部变量，链接器并不知道
    // sum 函数是一个全局引用
    // array 变量是一个全局引用
    return val;
}
// -----------------------------------------
// 文件 sum.c
int sum(int *a, int n) // 定义了一个全局函数
{
    int i, s = 0;
    // i 和 s 是局部变量，链接器并不知道
    for (i = 0; i < n; i++)
        s += a[i];
    
    return s;
}

链接器只知道非静态的全局变量/函数，不了解局部变量

局部非静态变量会保存在栈中
局部静态变量会保存在 .bss 或 .data 中