2020.08.14

//Given a 2D binary matrix filled with 0's and 1's, find the largest square cont
//aining only 1's and return its area. 
//
// Example: 
//
// 
//Input: 
//
//1 0 1 0 0
//1 0 1 1 1
//1 1 1 1 1
//1 0 0 1 0
//
//Output: 4
// Related Topics Dynamic Programming 
// 👍 3259 👎 80

//leetcode submit region begin(Prohibit modification and deletion)
class Solution {
    public int maximalSquare(char[][] matrix) {
        if(matrix.length == 0) return 0;
        int result = 0;
        int maxSide = 0;
        int[][] dp = new int[matrix.length + 1][matrix[0].length + 1];
        for (int i = 1; i < dp.length; i++) {
            for (int j = 1; j < dp[0].length; j++) {
                if (matrix[i-1][j-1] == '1') {
                    dp[i][j] = Math.min(Math.min(dp[i-1][j], dp[i][j-1]), dp[i-1][j-1]) + 1;
                    maxSide = Math.max(maxSide, dp[i][j]);
                    result = maxSide * maxSide;
                }
            }
        }
        return result;
    }
}
//leetcode submit region end(Prohibit modification and deletion)

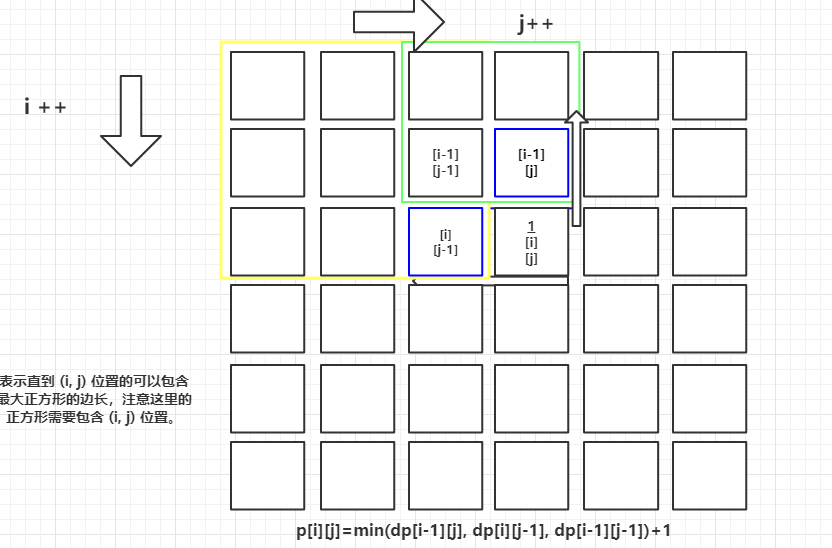
可以看成一个特别大的正方形，然后扣掉左上角和右小角(当前 arr[i][j])这样，其实决定的就是上，左，和上左所决定的三条线距离.

---

//Given a binary tree, return the inorder traversal of its nodes' values. 
//
// Example: 
//
// 
//Input: [1,null,2,3]
//   1
//    \
//     2
//    /
//   3
//
//Output: [1,3,2] 
//
// Follow up: Recursive solution is trivial, could you do it iteratively? 
// Related Topics Hash Table Stack Tree 
// 👍 3343 👎 140

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> result = new ArrayList<>();
        Stack<Integer> stack = new Stack<>();
        TreeNode cur = root;
        pushLeftUntilNull(cur, stack);

        while(!stack.isEmpty()){
            cur = stack.pop();
            list.add(cur.val);
            if(cur.right != null) {
                cur = cur.right;
                pushLeftUntilNull(cur, stack);
            }
        }
        
    }
    
    private void pushLeftUntilNull(TreeNode root, Stack<Integer> s){
        stack.push(root);
        while(root.left != null) {
            s.push(root.left);
            root = root.left;
        }
    }
}

节点全部都是入栈的,只不过每次都是入左臂所有节点, 综合起来就可以看成这样

其实左臂就已包含所有节点，不要片面的去考虑分支的方向，点就在那里，任凭你左链右链，它不增不减

---

Since 10^{i}$ \equiv 1（mod 9) ,then =>
(a_{i}$ * 10^{i}$ + a_{i-1}$ * 10^{i-1}$ + …) mod 9 = (a_{i}$ * 10^{i}$ mod 9 + a_{i-1}$ * 10^{i-1}$ mod 9 + …) mod 9
= (a_{i}$ + a_{i-1}$ + …) mod 9

https://leetcode.com/problems/add-digits/discuss/68580/Accepted-C%2B%2B-O(1)-time-O(1)-space-1-Line-Solution-with-Detail-Explanations

https://en.wikipedia.org/wiki/Digital_root#Congruence_formula

For base b (decimal case b = 10), the digit root of an integer is:

• dr(n) = 0 if n == 0
• dr(n) = (b-1) if n != 0 and n % (b-1) == 0
• dr(n) = n mod (b-1) if n % (b-1) != 0

or

• dr(n) = 1 + (n - 1) % 9

Note here, when n = 0, since (n - 1) % 9 = -1, the return value is zero (correct).

From the formula, we can find that the result of this problem is immanently periodic, with period (b-1).

Output sequence for decimals (b = 10):

~input: 0 1 2 3 4 ...
output: 0 1 2 3 4 5 6 7 8 9 1 2 3 4 5 6 7 8 9 1 2 3 ....

Henceforth, we can write the following code, whose time and space complexities are both O(1).

class Solution {
public:
    int addDigits(int num) {
        return 1 + (num - 1) % 9;
    }
};

---

Input: 00000010100101000001111010011100

Output: 00111001011110000010100101000000

Explanation: The input binary string 00000010100101000001111010011100 represents the unsigned integer 43261596, so return 964176192 which its binary representation is 00111001011110000010100101000000.

https://leetcode.com/problems/reverse-bits/discuss/54741/O(1)-bit-operation-C%2B%2B-solution-(8ms)

class Solution {
public:
    uint32_t reverseBits(uint32_t n) {
        n = (n >> 16) | (n << 16);  // swap the suffix 16 bits and prefix 16 bits position              
        n = ((n & 0xff00ff00) >> 8) | ((n & 0x00ff00ff) << 8); // go head but minimal the size  
        n = ((n & 0xf0f0f0f0) >> 4) | ((n & 0x0f0f0f0f) << 4);                                
        n = ((n & 0xcccccccc) >> 2) | ((n & 0x33333333) << 2);
        n = ((n & 0xaaaaaaaa) >> 1) | ((n & 0x55555555) << 1);
        return n;
    }
};

Explanation:
// 12345678
// 56781234
// 78563412
// 87654321